A virtuális billentyűs hangszerek MIDI vezérléssel szólaltathatók meg, és a hangmintavételezett eredeti hangszerek digitális reprodukciói (hangminták, samplings). Így saját MIDI hangszereink segítségével válogathatunk digitálisan reprodukált hangszereink közül. Ehhez szükséges egy vagy két MIDI-billentyűzet, egy MIDI-áramkörrel felszerelt orgonapedál, MIDI interface, igen jó minőségű hangkártya és jó paraméterekkel rendelkező számítógép megfelelő szoftverekkel, és egy szintén jó adottságokkal bíró erősítő, hangfalakkal, fejhallgatóval - és természetesen sok-sok hangminta...

Orgonák / Organs

Csembalók / Harpsichords

Harangjátékok / Carillons

A felszerelés

Hardware: HP Compaq nx8220 Notebook. Intel Pentium processor 1.73 GHz, 2 GB RAM. CPU 1733 MHz, 2981 MB/s / 792 MB/s M-Audio Audiophil Firewire hangkártya Roland Edirol UM-3EX USB MIDI interface

Software: Tascam Gigastudio3 MyOrgan

Billentyűzet Fatar Studiologic SL-880 Pro Billentyűzet 2 Miditech Midistudio 2 Pedal:MIDI-áramkörrel felszerelve

Erősítő: Pioneer A-221

Hangfal: SAL SilverSound 2610F, 150/250 W, 91 dB, 8 Ohm, 35-20000 Hz

bejátszások élő felvételek (nem MIDI-szerkesztővel készültek), a szoftverek belső hangrögzítésével készültek hullámformátumban (.wav) 44 Khz-es, 16 bites rögzítéssel. Az utómunkálatok Sony Sound Forge szoftverrel készültek. A tömörítés mp3-formátumú.

Bach: C-dúr prelúdium BWV 553/a Silbermann orgona (1721) hangminta / Silbermann organ (1721) sampling

Johann Sebastian Bach

Silbermann - 1721

Prelude in e minor BWV 533a 

Prelude in d minor BWV 539a 

Prelude in C major BWV 553a 

Prelude in d minor BWV 554a 

Sonatina from Actus tragicus BWV 106 (Alexandre Guilmant's transcription) 

Schnitger - 1704

Wer nur den lieben Gott laesst walten - choral prelude  

Jesus, meine Zuversicht - choral prelude  

Marcussen - 1965

Prelude in c minor BWV 549a 

Dietrich Buxtehude

Schnitger - 1704

Prelude in g minor BuxWV 149a 

Silbermann - 1721

Toccata in F major BuxWV 157a 

Louis-Nicolas Clérambault

Jullien - 1690

Suite du 2ème Ton - Plein jeu 

Suite du 2ème Ton - Trio 

Suite du 2ème Ton - Basse de cromorne 

Suite du 2ème Ton - Flutes 

Suite du 2ème Ton - Caprice pour les grands plein jeux 

François Couperin

Jullien - 1690

Messe pour les Couvents - Plein Jeu 

Messe pour les Couvents - Fugue sur la Trompette 

Messe pour les Couvents - Récit de Cromorne 

Louis Couperin

Jullien - 1690

Passacaille en sol mineur 

Johann Ernst Eberlin

Ehrlich - 1748

Prelude in d minor 

Johann Caspar Ferdinand Fischer

Silbermann - 1731

Ariadne Musica (1702) - Praeludium et Fuga no.1 in C major 

Ariadne Musica (1702) - Praeludium et Fuga no.2 in cis minor 

Ariadne Musica (1702) - Praeludium et Fuga no.3 in d minor 

Francesco Gasparini

Silbermann - 1722

Sonata per Elevazione 

Sonata in e minor 

Georg Friedrich Handel

Silbermann - 1722

Pieces for a musical clock - The Flight of Angels 

Pieces for a musical clock - Sonata 

Pieces for a musical clock - Minuet 

Pieces for a musical clock - Gigue 

Pieces for a musical clock - Air 

Pieces for a musical clock - Gigue 

Johann Erasmus Kindermann

Tauchmann - 1675

Harmonia organica (1645) - Praeambulum I-V. 

Harmonia organica (1645) - Praeambulum VI-X. 

Harmonia organica (1645) - Praeambulum XI-XIV. 

Narciso da Milano

Antegnati - 1636

Largo 

Sonata (Fuga) per l'Offertorio 

Georg Muffat

Ehrlich - 1748

Toccata prima in d from Apparatus Musico-Organisticus 

Gottlieb Muffat

Ehrlich - 1748

Toccata in C 

Toccata in g 

Toccata in e 

Fuga in d 

Guillaume-Gabriel Nivers

Jullien - 1690

Suite du 1er Ton - Prélude 

Suite du 1er Ton - Fugue 

Suite du 1er Ton - Récit de Cornet 

Suite du 1er Ton - Duo 

Suite du 1er Ton - Basse de Trompette 

Suite du 1er Ton - Écho 

Suite du 1er Ton - Fugue grave 

Suite du 1er Ton - Récit de Cromorne 

Suite du 1er Ton - Dialogue de Récit de Cromorne et de Cornet 

Suite du 1er Ton - Dialogue a deux Choeurs 

Johann Pachelbel

Silbermann - 1721

Prelude and Fugue in d minor 

Ciacona (Chaconne) in d minor 

Fugue in d minor 

Schnitger - 1704

Aria quinta from Hexachordum Apollinis 

Fuga cromatica in eminor 

Renaissance organ - 1587

Aria quinta from Hexachordum Apollinis 

Starck - 1699

Aria sexta (Aria Sebaldina) from Hexachordum Apollinis 

Henry Purcell

Marcussen - 1965

Trumpet Tune and Air 

Monsieur de Sainte-Colombe

Silbermann - 1721

Les pleurs (The Tears) from 'Le Tombeau des Regrets' (Pierre Gouin's transcription) 

John Stanley

Hart - 1809

Voluntary op. 5 No. 8 in d minor - Allegro 

Voluntary op. 5 No. 8 in d minor - Adagio 

Voluntary op. 5 No. 8 in d minor - Allegro 

Voluntary op. 5 No. 1 in C major - Adagio 

Voluntary op. 5 No. 1 in C major - Andante Trumpet 

Voluntary op. 5 No. 1 in C major - Slow 

Voluntary op. 6 No. 5 in d minor - Adagio 

Voluntary op. 6 No. 5 in D major - Andante Largo (Trumpet) 

Jan Pieterszoon Sweelinck

Marcussen - 1965

Echo Fantasia in a 

Johann Gottfried Walther

Silbermann - 1721

Concerto after Giulio Taglietti in B flat major - Adagio 

Concerto after Giulio Taglietti in B flat major - Allegro 

Concerto after Giulio Taglietti in B flat major - Adagio a 2 Clav. 

Concerto after Giulio Taglietti in B flat major - Allegro 

Ach Gott erhör mein Seufzen und Wehklage - choral prelude 

Alle Menschen müssen sterben - choral prelude 

Allein Gott in der Höh sei Ehr - choral prelude 

Das alte Jahr vergangen ist - choral prelude 

Domenico Zipoli

Mühleisen - 1997

Quattro versi in d 

Quattro versi in C 

BEVEZETÉS A TÖRTÉNETI HANGOLÁSOKBA

Michael Praetorius: Syntagma Musicum, 1619 - Theatrum instrumentorum , 25. metszet

A hangolás zeneesztétikai problémája: a zenematematika és a zenei érzékelés feszültsége, és az ennek kiküszöbölésére tett kísérlet: a temperálás A hangolás gyakorlati kivitelezése billentyűs hangszereken (clavichord, csembaló, zongora, orgona) Az orgonahangolás által meghatározott lokális kötöttségű zenekari hangolások Az egyenletes lebegésű temperálás történeti előzményei: az egyes hangolások Püthagoraszi, Középhangos I-IV, Arnout, Werckmeister I-III, Silbermann, Rameau, Kirnberger I-III, Vallotti, egyenletes lebegésű Az egyenletes lebegésú temperálás elterjedése és a történeti temperatúrák karakteriszikájának elvesztése.

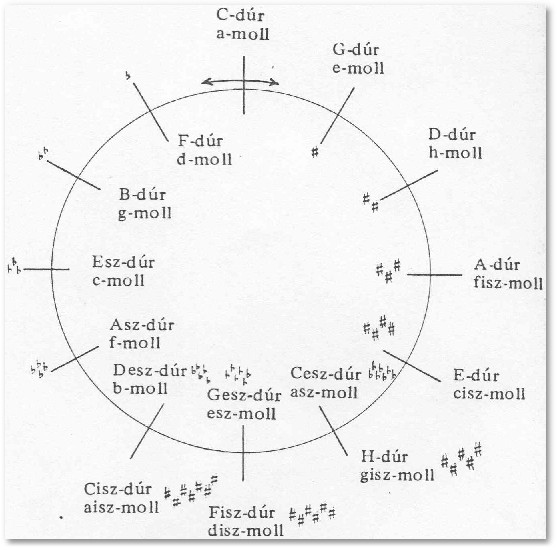
A kvintkör

1. Püthagoraszi:

Történetileg a püthagoraszi hangolások különböző fajtái jelennek meg először. Ezekben közös az, hogy a hangolás során a kiindulási hangtól tiszta kvinteket építenek fel. Ennek nyomán például az a hangról kezdve a következő kvintlánc lesz tisztán hangolva: a - e - h - fisz - cisz - gisz - disz/esz - b - f - c - g - d. Az utolsó kvint, a d - a viszony azonban szűk lesz. Ez az utolsó kvint arányszámát tekintve 531441:524288, azaz 1.0136 értékkel szűkebb a tiszta kvintnél. Az eltérés a püthagoraszi komma, melynek értéke 23.46 cent. Ez a hamis kvint az ún. püthagoraszi farkaskvint.

Ennek a típusú hangolásnak 12 fajtája lehetséges, aszerint, hogy a skála mely hangját tekintjük kiindulási pontnak. Mindezzel együtt három akkordstruktúra fordul elő: 8 akkord tiszta kvinttel és bő terccel, 3 akkord tiszta kvinttel és tiszta terccel, 1 akkord pithagoraszi farkaskvinttel és tiszta terccel. Az elsőként említett 8 akkordban lévő bő terc az ún. püthagoraszi terc, a lehető legtágabb fényes nagyterc. Ha a kvintlánc helyzete a - d (a fentebb leírt módon), akkor ebben a láncolatban tiszta kvinttel és püthagoraszi terccel szólal meg a Cisz-dúr, az Esz-dúr, az E-dúr, a Fisz-dúr, az Asz-dúr, az A-dúr, a B-dúr és a H-dúr. Tiszta kvinttel és tiszta terccel a C-dúr, az F-dúr és a G-dúr. Farkaskvintes akkord tiszta terccel a D-dúr.

A püthagoraszi hangolás a 16. században még használatos volt, és a modális hangrendszer miatt különösebb problémát nem jelentett, éppen a dúrhármasok hiánya miatt, szemben a későbbi dúr-moll tonalitás akkord-központú funkciós szemléletével.

A hangok megtalálása

A hangok és a hangkapcsolatok hatása teljességgel irracionális. Ugyanakkor a hangok és a hangkapcsolatok racionális rendet alkotnak, mely a hangközök matematikai leírásában ölt testet. Így a matematikai rend - látszólag - tökéletesen leírja a hangok racionális kapcsolatát, s ebből mintegy "kiolvasható" a hallott zene harmóniája. Nevezetessé és a hagyomány számára mértékadóvá vált egy püthagoreus töredék Jamblikhosztól, amely a hangközök matematikai arányai megtalálásának anekdotikus leírása:

"Egy alkalommal [Püthagorasz] éppen gondolataiban és feszült töprengésben merült el afelől, hogy nem tudna-e a hallásnak valami segítő eszközt kitalálni, ami erős és nincs tévedésnek alávetve, mint amilyen a látás esetében a függőón, a mérőrúd vagy éppenséggel a magasságmérő, a tapintás esetében pedig a mérlegkar vagy a súlyok kitalálása. Eközben egy kovácsműhely mellett ment el, s valami isteni véletlen folytán meghallotta a kalapácsokat, amint az üllőn a vasat kalapálták, s hogy egymásnak egy kapcsolat kivételével vegyesen, de összhangzóan adták a hangokat. Felismerte ugyanis bennük az oktávot, a kvintet, a kvartot. A kvart és a kvint közötti kapcsolatot önmagában disszonánsnak látta, de egyébként olyannak, ami alkalmas arra, hogy a köztük levő nagyságbeli különbséget kitöltse. Örvendezve, hogy terve isten segítségével sikerült, berohant a kovácsműhelybe, és sokféle kísérlet révén úgy találta, hogy a hangok különbségének oka a kalapácsok súlyában rejlik (.). Ezután a mértékeket és a kalapácsokkal a legteljesebben megegyező súlyokat pontosan megjegyezve hazatért."

Püthagorasz előbb egy cövekre erősített négy húrt, és azokra a megjegyzett mértékeknek megfelelő súlyokat függesztett. Az így megszólaló hangok a következők voltak:

"Úgy találta ugyanis, hogy a legnagyobb súlytól feszített húr  a legkisebb súly  feszítette húrral oktáv hangzatot ad. Az egyik tizenkét súlynyi volt, a másik pedig hat, s így kimondta, hogy az oktáv 2:1 arányú, amit már a súlyok is mutattak. (.) A legnagyobb a legkisebb mellett levővel (.) 3:2 (.). A legnagyobb viszont azzal, mely súlyban utána következett, a többinél pedig nagyobb volt, (.) 4:3."

12:6 = 2:1  kétszeres	oktáv
12:8 = 3:2  másfélszeres	kvint
12:9 = 4:3  négyharmados	kvart
12:8 x 12:9 = 3:2 x 4:3 = 9:8 kilencnyolcados	kvint és kvart közötti különbség [kis szekund]

Az így nyert arányokat átvitte a monochordra, és egyetlen húron megszólaltathatóvá váltak a hangarányok

A probléma

A kvintenként végighangolt püthagoraszi oktachord a 12. kvintnél azonban hamis lesz, ez az eltérés a püthagoraszi komma, és ez az érték okozza az ún. püthagoraszi farkaskvintet. A hangközök matematikai leírása, ezért nem tökéletes: a tiszta arányok betartása ellentmond a zenei érzékelésnek, és így jön létre az a feszültség, mely a zenematematika és a zene esztétikai tapasztalata között jelenik meg. A teljes püthagoraszi hangolás skálája:

Hang

C

C#

D

Eb

E

F

F#

G

G#

A

A#

B

C

Arányok

1/1

2187/2048

9/8

32/27

81/64

4/3

729/512

3/2

128/81

27/16

16/19

243/128

2/1

Cent

0

113.7

203.9

294.1

407.8

498

611.7

702

792.2

905.9

996.1

1109.8

1200

A középkor folyamán a többszólamúság megjelenését követően törvénnyé vált, hogy csak a tiszta kvintek alapján lehet hangolni, mert a 3:2-es arány áll a legközelebb az oktávhoz (2:1) és magához primhez (1:1) - ez a gondolkodásmód elsősorban teológiai megfontolásokon alapult: az arányszámok a Szentháromság tökéletességét szimbolizálták. Mivel a terc disszonanciának számított, és a korabeli zenei gyakorlat is így kezelte, ezért a későbbi dúrhármasok szerepe itt még tökéletesen irreleváns. A feszültséget azonban jól jelzi Johannes de Grocheo 1300 körül írt De musica című traktátusának egy helye: "A nagyterc két egész hangtávolságot magába foglaló konkordancia. Első hangjához úgy aránylik, mint 81 a 64-hez. Ezt némelyek konszonanciának is tartják, azok közé sorolják, mint pl. J. de Garlandia mester is. Minthogy azonban nem tökéletes konszonancia, és alkalmazása sérti a fület, mi mellőzzük." 1300 körül tehát a nagyterc korábbi státusza kérdéssé vált. A későbbiekben a nagytercet, elsősorban az angol John Dunstable (kb.1390-1453) és körének hatása miatt, újradefiniálták mint 5-ös arányszámú hangközt (5:4). Ez elmozdulást jelentett a tiszta zenematematikától a zenei érzékelés javára, ugyanis a 81:64 arány egészen pontosan 5.0625:4. Ez pedig már előrevetítette, hogy ha a terc konszonanciaként polgárjogot nyer, akkor a püthagoraszi elveken nyugvó hangolás elégtelenné válik. Így egy merőben új hangolás válik szükségessé.

Ez a probléma vetette fel a temperálás kérdését. A latin temperare első jelentése helyes mértékben vegyít, átvitt értelemben mérsékel, enyhít. Azaz a püthagoraszi hangolás feszültségteli pontját, a kommát enyhíteni kell. Ezt pedig nem lehet máshogy megtenni, mint a kommában, azaz a farkaskvintben megtestesülő "többletet" elosztani a skála hangjai között, és így kiküszöbölni a bő, püthagoraszi terceket. A kérdés éppen az volt, hogy miként lehet ezt megtenni.

Az első kísérlet a széles körben és igen hosszú ideig használatos ún. középhangos temperatúra lett. (Ld. 3. Középhangos temperatúrák)

Zenei illusztrációk:

Zenei illusztrációk: